Category: Quantum Computing

Posted on

21 = 3 * 7

…with high probability.
That joke was recycled, and in recent work, Bristol experimentalists have found a way to recycle photonic qubits to perform Shor’s algorithm using only lceil log Nrceil + 1 qubits. (Ok, so actually is was Kitaev who figured this out, as they are basically using Kitaev’s semi-classical QFT. But they found a way to do this with photons.) Further reductions on the number of qubits can be achieved by “compiling” to throw out the unused ones. In this case, we are left with a qubit and a qutrit. The feedback of the measurement is also replaced with the usual postselection. However, buried in the body of the paper is the main advance:

Our scheme therefore requires two consecutive photonic CNOT gates–something that has not previously been demonstrated–acting on qubit subspaces of the qutrit.

This is important progress, but until the factored numbers get a lot larger, the “size of number factored” yardstick is going to be a frustrating one. For example, how is it that factoring 143 on an NMR quantum computer takes only 4 qubits while factoring 15 takes 7?
Anyone have ideas for something more objective, like a quantum analogue of MIPS? (Incidentally, apparently MIPS is obsolete because of memory hierarchies.) Perhaps Grover’s algorithm would be good, as “compiling” is harder to justify, and noise is harder to survive.
Update:
In the comments, Tom Lawson points out the real significance of factoring 21. This is the smallest example of factoring in which the desired distribution is not uniformly random, thus making it possible to distinguish the successful execution of an experiment from the effects of noise.

Posted on

Greg Kuperberg: a paladin fighting against the ogres of hype

Nothing much to add here, but Greg Kuperberg has an excellent article at Slate which clarifies the power and limitations of quantum computers. The article is brief, accessible, and highly accurate. The next time a science journalist contacts you for a story, be sure to pass on a copy of this article as an exemplar of accurate, non-technical descriptions of quantum computing.

Posted on

Haroche and Wineland win Physics Nobel

David Wineland
Serge Haroche

The physics prize was shared between experimentalists Serge Haroche and David Wineland, longtime leaders in the study of atom-photon interaction.  In recent decades both have honed their techniques to meet the challenges and opportunities opened by “quantum information science” which aims to rebuild the theory and practice of communication and computation on quantum foundations.  This change of viewpoint was led by theorists, beginning with John Bell, and was initially regarded skeptically not only by information theorists and computer scientists, on whose turf it encroached, but even by many physicists, who saw a lot of theorizing, verging on philosophy, with little practice to back it up.  Haroche, working often with Rydberg atoms and microwave cavities, and Wineland, with trapped ions and optical fields, took the new approach seriously, and over many years have provided much of the solid foundation of practice that has by now has earned the field the right to be taken seriously.  At the same time both researchers have done their part to restrain the inevitable hype.    A decade and a half ago Haroche, in articles like “Quantum Computing: Dream or Nightmare” pointed out how difficult building a quantum computer would be, while always believing it possible in principle, and in the mean time produced, with his group, an impressive stream of experimental results and technical improvements  that made it ever more practical.  In the same vein, Wineland, when asked if ion traps were the right hardware for building a quantum computer, answered that whatever advantage they had was like being 10 feet ahead at the start of a 10 mile race.  Then like Haroche he went ahead making steady progress in the control and measurement of individual particles, with applications quite apart from that distant goal.
Both men are consummate experimentalists, finding and adapting whatever it takes.  I visited Wineland’s lab about a decade ago and noticed a common dishwashing glove (right handed and light blue, as I recall) interposed between the ion trap’s optical window and a CCD camera focused the ions within.   I asked David what its function was among all the more professional looking equipment.   He said this particular brand of gloves happened to be quite opaque with a matte black inside as good as anything he could get from an optics catalog, meanwhile combining moderate flexibility with sufficient rigidity to stay out of the way of the light path, unlike, say, a piece of black velvet.  Indeed the cut-off thumb fitted nicely onto the optical window, and the wrist was snugly belted around the front of the camera, leaving the fingers harmlessly but ludicrously poking out at the side.  The physics Nobel has occasioned a lot of press coverage, much of it quite good in conveying the excitement of quantum information science, while restraining unrealistic expectations.   We especially like Jason Palmer’s story from earlier this year which the BBC resurrected to explain a field which this Nobel has suddenly thrust into the limelight.   We congratulate Haroche and Wineland as deserving and timely winners of this first Nobel given to people who could fairly be described, and would now describe themselves, as quantum information scientists.
 

Posted on

Throwing cold water on the Quantum Internet

There has been a lot of loose talk lately about a coming “Quantum Internet”. I was asked about it recently by a journalist and gave him this curmudgeonly answer, hoping to redirect some of the naive enthusiasm:
…First let me remark that “quantum internet” has become a bit of a buzzword that can lead to an inaccurate idea of the likely role of quantum information in a future global information infrastructure.  Although quantum concepts such as qubit and entanglement have revolutionized our understanding of the nature of information, I believe that the Internet will remain almost entirely classical, with quantum communication and computation being used for a few special purposes, where the unique capabilities of quantum information are needed.  For other tasks, where coherent control of the quantum state is not needed, classical processing will suffice and will remain cheaper, faster, and more reliable for the foreseeable future.  Of course there is a chance that quantum computers and communications links may some day become so easy to build that they are widely used for general purpose computing and communication, but I think it highly unlikely.
Would the quantum internet replace the classical one, or would the two somehow coexist?
As remarked above, I think the two would coexist, with the Internet remaining mostly classical. Quantum communication will be used for special purposes, like sharing cryptographic keys, and quantum computing will be used in those few situations where it gives a significant speed advantage (factoring large numbers, some kinds of search, and the simulation of quantum systems), or for the processing of inherently quantum signals (say from a physics experiment).
Would quantum search engines require qubits transmitted between the user’s computer and the web searcher’s host? Or would they simply use a quantum computer performing the search on the host machine, which could then return its findings classically?
It’s not clear that quantum techniques would help search engines, either in transmitting the data to the search engine, or in performing the search itself. Grover’s algorithm (where coherent quantum searching gives a quadratic speedup over classical searching) is less applicable to the large databases on which search engines operate, than to problems like the traveling salesman problem, where the search takes place not over a physical database, but over an exponentially large space of virtual possibilities determined by a small amount of physical data.
On the other hand, quantum techniques could play an important supporting role, not only for search engines but other Internet applications, by helping authenticate and encrypt classical communications, thereby making the Internet more secure. And as I said earlier, dedicated quantum computers could be used for certain classically-hard problems like factoring, searches over virtual spaces, simulating quantum systems, and processing quantum data.
When we talk about quantum channels do we mean a quantum communication link down which qubits can be sent and which prevents them decohering, or are these channels always an entangled link? …
A quantum channel of the sort you describe is needed, both to transmit quantum signals  and to share entanglement. After entanglement has been shared, if one has a quantum memory, it can be stored and used later in combination with a classical channel to transmit qubits.  This technique is called quantum teleportation (despite this name, for which I am to blame, quantum teleportation cannot be used for transporting material objects).
But could we ever hope for quantum communication in which no wires are needed – but entanglement handles everything?
The most common misconception about entanglement is that it can be used to communicate—transmit information from a sender to a receiver—perhaps even instantaneously. In fact it cannot communicate at all, except when assisted by a classical or quantum channel, neither of which communicate faster than the speed of light. So a future Internet will need wires, radio links, optical fibers, or other kinds of communications links, mostly classical, but also including a few quantum channels.
How soon before the quantum internet could arrive?
I don’t think there will ever be an all-quantum or mostly-quantum internet. Quantum cryptographic systems are already in use in a few places, and I think can fairly be said to have proven potential for improving cybersecurity. Within a few decades I think there will be practical large-scale quantum computers, which will be used to solve some problems intractable on any present or foreseeable classical computer, but they will not replace classical computers for most problems. I think the Internet as a whole will continue to consist mostly of classical computers, communications links, and data storage devices.
Given that the existing classical Internet is not going away, what sort of global quantum infrastructure can we expect, and what would it be used for?  Quantum cryptographic key distribution, the most mature quantum information application, is already deployed over short distances today (typically < 100 km).   Planned experiments between ground stations and satellites in low earth orbit promise to increase this range several fold.  The next and more important stage, which depends on further progress in quantum memory and error correction,  will probably be the development of a network of quantum repeaters, allowing entanglement to be generated between any two nodes in the network, and, more importantly, stockpiled and stored until needed.  Aside from its benefits for cybersecurity (allowing quantum-generated cryptographic keys to be shared  between any two nodes without having to trust the intermediate nodes) such a globe-spanning quantum repeater network will have important scientific applications, for example allowing coherent quantum measurements to be made on astronomical signals over intercontinental distances.  Still later, one can expect full scale quantum computers to be developed and attached to the repeater network.  We would then finally have achieved a capacity for fully general processing of quantum information, both locally and globally—an expensive, low-bandwidth quantum internet if you will—to be used in conjunction with the cheap high-bandwidth classical Internet when the unique capabilities of quantum information processing are needed.

Posted on

Lucky 13 paper dance!

Having recently rediscovered arxiv.org/submit, I thought I’d mention a few papers to come out of team UW.
Two particularly exciting single-author papers are from students here.
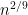Kamil Michnicki has developed a 3-d stabilizer code on n qubits with an energy barrier that scales as n^{2/9}. By contrast, such a result is impossible in 2-d, and the best energy barrier previously obtained in 3-d was O(log n) from Haah’s breakthrough cubic code. Sadly, this code appears not to have the thermal stability properties of the 4-d toric code, but it nevertheless is an exciting step towards a self-correcting quantum memory.

1208.3496: 3-d quantum stabilizer codes with a power law energy barrier
Kamil Michnicki

David Rosenbaum has written a mostly classical algorithms paper about the old problem of group isomorphism: given two groups 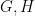G,H specified by their multiplication tables, determine whether they are isomorphic. The problem reduces to graph isomorphism, but may be strictly easier. Since any group with |G|=n has a generating set of size leq log_2(n), it follows that the problem can be solved in time n^{log(n)+O(1)}. While faster algorithm have been given in many special cases, the trivial upper bound of n^{log(n)} has resisted attack for decades. See Gödel’s Lost Letter for some discussion. The particular classes of groups considered to be hardest have been the nilpotent (or more generally solvable) groups, since paradoxically the rigidity of highly non-abelian groups (e.g. simple groups) makes them easier to address. David found a polynomial speedup for solvable groups, thus making the first progress on this problem since the initial n^{log(n)} algorithms.

1205.0642: Breaking the 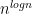n^{log n} Barrier for Solvable-Group Isomorphism
David Rosenbaum

Lukas Svec (together with collaborators) also has a nice way of improving the Gottesman-Knill simulations that have been so effective in estimating FTQC thresholds. Gottesman-Knill allows mixtures of Clifford unitaries to be simulated classically, which seems as thought it should be only be effective for simulating unital noise. However, throwing away a qubit and replacing it with the |0rangle state can also be encompassed within the Gottesman-Knill approach. This insight allows them to give much better simulations of amplitude-damping noise than any previous approach.

1207.0046: Approximation of real error channels by Clifford channels and Pauli measurements
Mauricio Gutiérrez, Lukas Svec, Alexander Vargo, Kenneth R. Brown

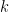There have also been two papers about the possibilities of two dimensions. David has a paper explaining how a general circuit with arbitrary two-qubit interactions on n qubits can be simulated in a 2-d architecture by using n^2 qubits. If only k gates happen per time step, then 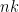nk qubits suffice. The key trick is to use classical control to perform teleportation chains, an idea of whose provenance I’m unclear on, but which is based in part on MBQC and in part on a remarkable paper of Terhal and Divincenzo.

1205.0036: Optimal Quantum Circuits for Nearest-Neighbor Architectures
David Rosenbaum

Examining particular algorithms can enable more dramatic speedups, and by examining Shor’s algorithm, Paul Pham was able to reduce the depth to polylogarithmic, surprisingly finding an improved implementation of the most well-studied of quantum algorithms.

1207.6655: A 2D Nearest-Neighbor Quantum Architecture for Factoring
Paul Pham, Krysta M. Svore

David and I also have a joint paper on an alternate oracle model in which one input to the oracle is supplied by the user and a second input is random noise. While in some cases (e.g. a Grover oracle that misfires) this does not lead to quantum advantages, we find that in other cases, quantum computers can solve problems in a single query that classical computers cannot solve with unlimited queries. Along the way, we address the question of when some number of (quantum or classical) queries yield no useful information at all about the answer to an oracle problem.

1111.1462: Uselessness for an Oracle Model with Internal Randomness
David Rosenbaum, Aram W. Harrow

My co-blogger Steve has also been active. Steve and his co-authors (does that make them my step-co-authors?) have written perhaps the definitive work on how to estimate approximately low-rank density matrices using a small number of measurements.

1205.2300: Quantum Tomography via Compressed Sensing: Error Bounds, Sample Complexity, and Efficient Estimators
Steven T. Flammia, David Gross, Yi-Kai Liu, Jens Eisert

Steve, together with Ghost Pontiff Dave and Dave’s former student Gregory Crosswhite have also posted

1207.2769: Adiabatic Quantum Transistors
Dave Bacon, Steven T. Flammia, Gregory M. Crosswhite

This paper proposes a deeply innovative approach to quantum computing, in which one adiabatically transforms one simple spatially-local Hamiltonian to another. Unlike previous approaches, it seems to have a chance of having some compelling fault-tolerance properties, although analyzing this remains challenging.
Steve and I also have a brief note (arXiv:1204.3404) relevant to my ongoing debate with Gil Kalai (see here, here, here, here, here, here or here) in which we point out counterexamples to one of Gil’s conjectures. This post specifically contains more discussion of the issue.
Finally, I’ve been clearing out a lot of my unpublished backlog this year.
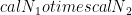My co-authors and I wrote a short paper explaining the main ideas behind the superactivation of zero-error capacity. The principle is similar to that found in all of the additivity violations based on random quantum channels: we choose a correlated distribution over channels {cal N}_1, {cal N}_2 in a way that forces {cal N}_1otimes {cal N}_2 to have some desired behavior (e.g. when acting on a particular maximally entangled state). At the same time, apart from this constraint, the distribution is as random as possible. 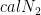Hopefully we can then show that any single-copy use of {cal N}_1 or {cal N}_2 has low capacity, or in our case, zero zero-error capacity. In our case, there are a few twists, since we are talking about zero-error capacity, which is a fragile property more suited to algebraic geometry than the usual approximate techniques in information theory. On the other hand, this means that at many points we can show that properties hold with probability 1. 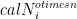The other nontrivial twist is that we have to show that not only {cal N}_i has zero zero-error capacity (yeah, I know it’s a ridiculous expression) but {cal N}_i^{otimes n} does for all n. This can be done with some more algebraic geometry (which is a fancy way of saying that the simultaneous zeroes of a set of polynomials has measure equal to either 0 or 1) as well as the fact that the property of being an unextendible product bases is stable under tensor product.

1109.0540:Entanglement can completely defeat quantum noise
Jianxin Chen, Toby S. Cubitt, Aram W. Harrow, Graeme Smith

One paper that was a fun bridge-building exercise (with a nice shout out from Umesh Vazirani/BILL GASARCH) was a project with quantum information superstar Fernando Brandão as well as a pack of classical CS theorists. My part of the paper involved connections between QMA(2) and optimizing polynomials over mathbb{R}^n. For example, if 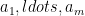a_1,ldots, a_m are the rows of a matrix 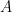A, then define |A|_{2rightarrow 4} = max_{|x|_2=1} |Ax|_4 = max_{|x|_2=1} (sum_{i=1}^m |langle a_i, xrangle|^4)^{1/4}. 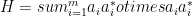Taking the fourth power we obtain the maximum energy attainable by product states under the Hamiltonian H = sum_{i=1}^m a_i a_i^* otimes a_i a_i^*. Thus, hardness results and algorithms can be ported in both directions. One natural algorithm is called “the Lasserre SDP hierarchy” classically and “optimizing over 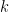k-extendable states” quantumly, but in fact these are essentially the same thing (an observation dating back to a 2003 paper of Doherty, Parrilo, and Spedalieri). There is much more to the paper, but I’ll leave it at that for now.

1205.4484: Hypercontractivity, Sum-of-Squares Proofs, and their Applications
Boaz Barak, Fernando G.S.L. Brandão, Aram W. Harrow, Jonathan A. Kelner, David Steurer, Yuan Zhou

Another big collaboration taking me out of my usual areas was this paper on quantum architecture. Suppose that our quantum computer is comprised of many small nodes (say ion traps), connected by long-range links (say optical fibers), as has been recently advocated. This computer would not be stuck with a 2-d topology, but could be connected in any reasonably low-degree configuration. Our paper shows that a hypercube topology (among many other possibilities) is enough to simulate general quantum circuits. This enables parallelized versions of Grover search that finally (in my opinion) address the problem raised by Grover and Rudolph about the memory requirements for the “best” known collision and element-distinctness algorithms. As a result, we find space-time tradeoffs (assuming this hypercube topology) for collision and element distinctness of 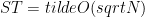ST=tilde O(sqrt N) and ST=tilde O(N) respectively.

1207.2307: Efficient Distributed Quantum Computing
Robert Beals, Stephen Brierley, Oliver Gray, Aram W. Harrow, Samuel Kutin, Noah Linden, Dan Shepherd, Mark Stather

The next paper was on more familiar territory. Together with my former PhD student Richard Low (and building on the work of Dahlsten, Oliveira and Plenio), I proved that random quantum circuits are approximate unitary 2-designs in 0802.1919. Later Fernando Brandão and Michal Horodecki improved this to show that random quantum circuits are approximate unitary 3-designs in 1010.3654 (achieving a sweet oracle speedup in the process). Teaming up with them I expected maybe to reach 5-designs, but in the end we were able to get arbitrary 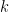k-designs on n qubits with circuits of length {rm poly}(n,k).

1208.0692 Local random quantum circuits are approximate polynomial-designs
Fernando G. S. L. Brandão, Aram W. Harrow, Michal Horodecki

Finally, one more paper came out of my classical CS dabbling. Together with classical (but quantum curious) theorists Alexandra Kolla and Leonard Schulman, we found a cute combinatorial result in our failed bid to refute the unique games conjecture on the hypercube. Our result concerns what are called maximal functions. Hardy and Littlewood introduced these by talking about cricket; here is a contemporary version. Imagine that you are a Red Sox fan whose happiness at any given time depends on what fraction of the last n games the Red Sox have won against the Yankees. Fortunately, you are willing to choose n differently from day to day in order to maximize your happiness. 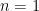For example, if the Red Sox won the last game, you take n=1 and your happiness is 100%. If they won 3 out of the last 5 games, you could take 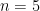n=5 and obtain happiness 60%. The maximal operator takes the win-loss series and transforms it into the happiness function. (A similar principle is at work when the loser of rock-paper-scissors proposes best 3-out-of-5, and then best 4-out-of-7, etc.) In our paper, we bound how much the maximal operator can increase the 2-norm of a function when it acts on functions on the hypercube, and the maximization is taken not over intervals, but over Hamming spheres in the hypercube. Along the way, we prove some bounds on Krawtchouk polynomials that seem so simple and useful I feel we must have overlooked some existing paper that already proves them.

1209.4148: Dimension-free L2 maximal inequality for spherical means in the hypercube
Aram W. Harrow, Alexandra Kolla, Leonard J. Schulman

Posted on

QIP 2013

QIP is in Beijing this time from Jan 21-25, 2013. And the call for papers has just been posted.

  • Submission deadline for talks: October 5, 2012
  • Notification for talk submissions: November 9, 2012
  • Submission deadline for posters: November 16, 2012
  • Notification for poster submissions: November 26, 2012

The submission guidelines continue to slowly evolve. Last year called for “2-3 pages in a reasonable font” and this year is a somewhat more precise “up to 3 pages in 11pt font with reasonable margins, not including references”. From my experience on PCs in the past (I’m not on the PC this year, though), I’ll mention that these short submissions sometimes are very good, but sometimes aren’t addressed at the key questions that the PC will want to consider, such as:

  • What is the key result?
  • How does it compare with previous work on this subject? And how does it fit into the broader context of other research?
  • What are the technical innovations necessary to achieve it, and possibly to overcome obstacles that stopped people before?
  • (If the topic area is unconventional, or the submission is about a newly invented problem.) Why is this a good area for people to study?

These are kind of basic, but it’s surprising how many good results are undermined by not explaining these points well.
Another feature of the CFP to notice is that authors are strongly recommended to link to a version of their paper on their arxiv, or to include a long version of their paper as an attachment. The idea here is that if a result is not ready to go on the arxiv, then it’s less likely to be correct. There was debate about making it mandatory to post a full version on the arxiv, but this idea was dropped because many people felt that this way we might miss out on the freshest results.
A related concern is about keeping the barriers to submitting to QIP low. Of course, travel is always a barrier, but hopefully we shouldn’t waste a lot of people’s time with elaborate submission requirements if we expect the acceptance rate to be around 20%. I think the current requirements are reasonable, as long as people don’t stress too much about making a special short version, e.g. by writing something informal about why the paper should be accepted and referring liberally to the long version instead of trying to pack as much as possible in three pages. But I can imagine other systems as well. What do you think about the way QIP is being run right now?

Posted on

Threading the needle of mathematical consistency

The latest round of the debate between Aram and Gil Kalai is now up over at Goedel’s Lost Letter.
I realize that I’m preaching to the choir at this venue, but I thought I would highlight Aram’s response. He nicely sums up the conundrum for quantum skeptics with a biblical allusion:

…Gil and other modern skeptics need a theory of physics which is compatible with existing quantum mechanics, existing observations of noise processes, existing classical computers, and potential future reductions of noise to sub-threshold (but still constant) rates, all while ruling out large-scale quantum computers. Such a ropy camel-shaped theory would have difficulty in passing through the needle of mathematical consistency.

One of the things that puzzles me about quantum skeptics is that they always seem to claim that there is an in principle reason why large-scale quantum computation is impossible. I just completely fail to see how they infer this from existing lines of evidence. If the skeptics would alter their argument slightly, I might have some more sympathy. For example, why don’t we power everything with fusion by now? Is it because there is a fundamental principle that prevents us from harnessing fusion power? No! It just turned out to be much harder than anyone thought to generate a self-sustaining controlled fusion reaction. If skeptics were arguing that quantum computers are the new fusion reactors, then I can at least understand how they might think that in spite of continuing experimental progress. But in principle impossible? It seems like an awfully narrow needle to thread.

Posted on

QIP 2012 videos!

The long awaited videos from QIP 2012 are now online.
Somewhat. If you see a video that you want that isn’t online, then tell the speaker to sign the release form! I’m looking at you Bravyi, Greiner, Landahl and Popescu! (And others.)
If you haven’t seen them before, then you should check out the talks by Haah (on 3-d local stabilizer codes) and Arad (on an improved 1-d area law).

Posted on

300

Credit: Britton/NIST

One of the more exciting prospects for near-term experimental quantum computation is to realize a large-scale quantum simulator. Now getting a rigorous definition of quantum simulator is tricky, but intuitively the concept is clear: we wish to have quantum systems in the lab with tunable interactions which can be used to simulate other quantum systems that we might not be able to control, or even create, in their “native” setting. A good analogy is a scale model which might be used to simulate the fluid flow around an airplane wing. Of course, these days you would use a digital simulation of that wing with finite element analysis, but in the analogy, that would correspond to using a fault-tolerant quantum computer, a much bigger challenge to realize.
We’ve highlighted the ongoing progress in quantum simulators using optical lattices before, but now ion traps are catching up in interesting ways. They have literally leaped into the next dimension and trapped an astounding 300 ions in a 2D trap with a tunable Ising-like coupling. Previous efforts had a 1D trapping geometry and ~10 qubits; see e.g. this paper (arXiv).
J. W. Britton et al. report in Nature (arXiv version) that they can form a triangular lattice of beryllium ions in a Penning trap where the strength of the interaction between ions i and j can be tuned to J_{i,j} sim d(i,j)^{-a} for any 0<a<3, where d(i,j) is the distance between spins i and j by simply changing the detuning on their lasers. (They only give results up to a=1.4 in the paper, however.) They can change the sign of the coupling, too, so that the interactions are either ferromagnetic or antiferromagnetic (the more interesting case). They also have global control of the spins via a controllable homogeneous single-qubit coupling. Unfortunately, one of the things that they don’t have is individual addressing with the control.
In spite of the lack of individual control, they can still turn up the interaction strength beyond the point where a simple mean-field model agrees with their data. In a) and b) you see a pulse sequence on the Bloch sphere, and in c) and d) you see the probability of measuring spin-up along the z-axis. Figure c) is the weak-coupling limit where mean-field holds, and d) is where the mean-field no longer applies.
Credit: Britton/NIST

Whether or not there is an efficient way to replicate all of the observations from this experiment on a classical computer is not entirely clear. Of course, we can’t prove that they can’t be simulated classically—after all, we can’t even separate P from PSPACE! But it is not hard to imagine that we are fast approaching the stage where our quantum simulators are probing regimes that can’t be explained by current theory due to the computational intractability of performing the calculation using any existing methods. What an exciting time to be doing quantum physics!