
One of the more exciting prospects for near-term experimental quantum computation is to realize a large-scale quantum simulator. Now getting a rigorous definition of quantum simulator is tricky, but intuitively the concept is clear: we wish to have quantum systems in the lab with tunable interactions which can be used to simulate other quantum systems that we might not be able to control, or even create, in their “native” setting. A good analogy is a scale model which might be used to simulate the fluid flow around an airplane wing. Of course, these days you would use a digital simulation of that wing with finite element analysis, but in the analogy, that would correspond to using a fault-tolerant quantum computer, a much bigger challenge to realize.
We’ve highlighted the ongoing progress in quantum simulators using optical lattices before, but now ion traps are catching up in interesting ways. They have literally leaped into the next dimension and trapped an astounding 300 ions in a 2D trap with a tunable Ising-like coupling. Previous efforts had a 1D trapping geometry and ~10 qubits; see e.g. this paper (arXiv).
J. W. Britton et al. report in Nature (arXiv version) that they can form a triangular lattice of beryllium ions in a Penning trap where the strength of the interaction between ions and
can be tuned to
for any
, where
is the distance between spins
and
by simply changing the detuning on their lasers. (They only give results up to
in the paper, however.) They can change the sign of the coupling, too, so that the interactions are either ferromagnetic or antiferromagnetic (the more interesting case). They also have global control of the spins via a controllable homogeneous single-qubit coupling. Unfortunately, one of the things that they don’t have is individual addressing with the control.
In spite of the lack of individual control, they can still turn up the interaction strength beyond the point where a simple mean-field model agrees with their data. In a) and b) you see a pulse sequence on the Bloch sphere, and in c) and d) you see the probability of measuring spin-up along the z-axis. Figure c) is the weak-coupling limit where mean-field holds, and d) is where the mean-field no longer applies.

Whether or not there is an efficient way to replicate all of the observations from this experiment on a classical computer is not entirely clear. Of course, we can’t prove that they can’t be simulated classically—after all, we can’t even separate P from PSPACE! But it is not hard to imagine that we are fast approaching the stage where our quantum simulators are probing regimes that can’t be explained by current theory due to the computational intractability of performing the calculation using any existing methods. What an exciting time to be doing quantum physics!

O brave new quantum world!
It’s good to see smoke coming from the Pontiffs’ Vatican chimney and thank you, Steve, for this fine summary of some outstandingly interesting research. secant variety of a Segre variety (that is, a matrix product state of rank-
secant variety of a Segre variety (that is, a matrix product state of rank- ). For systems of 300 spins, it is numerically feasible to integrate curves for ranks
). For systems of 300 spins, it is numerically feasible to integrate curves for ranks 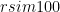 or so.
or so.
From a simulationist/geometer point-of-view, this experiment has intriguing aspects beyond those mentioned in the article. Let us suppose that we simulate the experiment’s wave-function as the (numerically computed) integral curve of a Hamiltonian trajectory. For reason of numerical efficiency, we can pullback the physics onto a rank-
A natural question is, how large a state-space rank is required to accurately simulate the experiment? The answer (it seems to me) is likely to depend upon a key parameter of the experiment, namely, the (parasitic) noise operations that act upon the qubits … because these operations generically act to compress the system’s dynamical trajectories onto the above-mentioned varietal state-spaces.
It might perhaps be the case — and it is a fundamentally important question to investigate — that the condensed matter regimes that are hardest to simulate numerically, are precisely the regimes that are most sensitive to (parasitic) noise operations.
Thus this experiment opens a new world not only to fundamental quantum physics experiments, but also (and essentially equivalently) to the fundamental validation of algorithms. It’s exciting!
Hi Steve,
This is indeed exciting. As you mentioned, the question if observations from this or similar experiments can be replicated by classical computers leads us to notorious computational complexity issues, perhaps a better question is if this or similar experiments can be simulated by a quantum computer running a bounded number of computer cycles. Is it?
A class of questions related to Gil’s (to which I don’t know the answer) is: How might one use quantum simulation algorithms to speed-up the simulation of non-equilibrium and/or finite-temperature dynamics, so as to estimate (for example) the spin system’s heat conductivity?
Hi Gil,
I’m quite confident that the answer is “yes”, the experiment can be simulated on a quantum computer in a bounded number of steps. At the very worst case, experiments like these always fit inside of PSPACE (once you suitably abstract them), hence for a fixed input size you only need a bounded number of computational steps to simulate everything.
Hi Steve,
Of course we need to be careful if we try to apply computational complexity terminology and insights for real life situation.
Everything we do is with finite input size so your type of reasoning make every real life application of computational complexity meaningless including your question from the post “Whether or not there is an efficient way to replicate all of the observations from this experiment on a classical computer is not entirely clear. ”
My question is about a small number of quantum computer cycles (2, 3, 5) which will NOT scale up when you replace 300 by, say, 3,000. Of course if by “bounded” we allow 2^300 or even 300^2 we miss the entire point.
Thanks for the clarification; I had indeed misunderstood your question. Let us abstract away the details of the experiment, and suppose that they are working with n spins. They want to prepare the ground state of, and observe the dynamics of, a system with an Ising-type interaction that decays with distance, a homogeneous single-qubit control field, and single-qubit measurements in the computational basis. Then I believe you are asking whether there is a constant-depth quantum circuit to simulate the distribution of measurement outcomes. My guess in that case is no, but I can’t be certain. The so-called “no fast-forwarding theorem” (Thm. 3 in quant-ph/0508139) is a no-go theorem which is relevant in the general case, but since this is a specific instance I don’t know that we can say anything definitive.
“They want to prepare the ground state …”
Hmmm … it’s not clear this system (or any similar system) affords methods for preparing a ground state that are general, natural, and robust.
However, it’s a system well-suited to studying thermodynamical equations of state and/or transport coefficients … and these are the properties that one generally wishes to know.