Warning: this idiosyncratic list of reading material is in no way meant to be comprehensive nor does is it even guaranteed to focus on the most important papers concerning graph isomorphism. Suggestions for other papers to add to the list are greatly appreciated: leave a comment!
The graph isomorphism problem is an intriguing problem. A graph is a set of vertices along with the edges connecting these vertices. The graph isomorphism problem is to determine, given the description of two graphs, whether these descriptions are really the same graph. For example, is it possible to relabel and move the vertices in the two graphs below so as to make them look the same?


Give up? Okay, well it wasn’t so hard this one, but yes these graphs are isomorphic 🙂 Usually we aren’t given two pictures of the graphs, but instead are given a succinct description of what vertices are connected to each other. This is given by either and adjacency matrix or and adjacency list. The adjacency matrix of a graph with  vertices is a
vertices is a 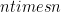 matrix whose
matrix whose 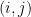 th entry is the number of edges from vertex
th entry is the number of edges from vertex 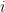 to
to  . An algorithm is efficient for the graph isomorphism problem if it takes a running time that is polynomial in the number of vertices of the graphs involved.
. An algorithm is efficient for the graph isomorphism problem if it takes a running time that is polynomial in the number of vertices of the graphs involved.
One reason why graph isomorphism is interesting is it current status in computational complexity. It is not likely to be NP-complete (as this would cause a collapse of the polynomial hierarchy), yet despite a considerable amount of work, there is no known polynomial time algorithm for this problem. Graph isomorphism is known to be in the complexity class NP intersect co-AM, which is kind of similar to where the decision version of factoring lies (NP intersect co-NP.) This similarity, along with the fact that a natural generalization of the quantum problem solved by factoring (the hidden subgroup problem) is related to graph isomorphism (efficiently solving the hidden subgroup problem for the symmetric group would yield an efficient algorithm for graph isomorphism) has led to the hope that quantum computers might be able to efficiently solve graph isomorphism. I will admit, over the years, I have slowly but surely developed quite a severe of the graph isomorphism disease, albeit my case appears to be of the quantum kind. Like any disease, it is important to spread the disease. So here is a collection of readings about the graph isormophism problem.
One interesting aspect of the graph isomorphism problem is that there are classes of graphs for which there do exist efficient polynomial time algorithms for deciding isomorphism of graphs in these classes. Because one can get downbeat pretty quickly bashing your head against the problem, I think it would be nice to start out with an easy case: tree isomorphism. The efficient algorithm for this is usually attributed to Aho, Hopcroft and Ullman (1974), but I really like
- “Tree Isomorphism Algorithms: Speed vs. Clarity” by Douglas M. Campbell and David Radford, Mathematics Magazine, Vol. 64, No. 4 (Oct., 1991), pp. 252-261 (paper here)
It’s a fun easy read that will get you all excited about graph isomorphism, I’m sure.
Okay well after that fun start, maybe staying within the realm of polynomial time algorithms continues to feel good. One of the classic ways to attempt to solve graph isomorphism is as follows: compute the eigenvalues of the adjacency matrices of the two graphs, and sort these eigenvalues. If the eigenvalues are different, then the graphs cannot be isomorphic. Why? Well if the graphs are isomorphic, there exists a 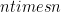 permutation matrix
permutation matrix 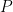 (a matrix made of zeros and ones that has only a single one in each row and in each column) such that
(a matrix made of zeros and ones that has only a single one in each row and in each column) such that  (here
(here 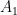 and
and  are the adjacency matrices of the two graphs.) And recall that the eigenvalues of
are the adjacency matrices of the two graphs.) And recall that the eigenvalues of 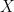 and
and  are the same for invertible matrices
are the same for invertible matrices 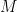 . Thus isomorphic graphs must have the same eigenvalues. Note, however, that this does not imply that non-isomorphic graphs have different eigenvalues. For example, consider the following two trees
. Thus isomorphic graphs must have the same eigenvalues. Note, however, that this does not imply that non-isomorphic graphs have different eigenvalues. For example, consider the following two trees


These trees are clearly not isomorphic. On the other hand, if you take the eigenvalues of their adjacency matrices you will find out that they are both given by
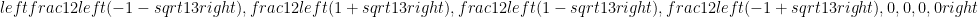 .
.
So there exists isospectral (same eigenvalues of the adjacency matrix) but non-isomorphic graphs. Thus taking the eigenvalues of the graph isn’t enough to distinguish non-isomorphic graph. In practice, however, this usually works pretty good. Further, if we consider graphs where the maximum multiplicity of the eigenvalues (recall that an eigenvalue may appear multiple times in the list of eigenvalues of a matrix—the multiplicity is the number of times an eigenvalue appears) is bounded (that is the multiplicity does not grow with the graph size), then there is an efficient algorithm for graph isomorphism. This was first shown for multiplicity one graphs, i.e. where all the eigenvalues are distinct, by Leighton and Miller. This work is unpublished, but you can find the hand written notes at Gary Miller’s website:
- “Certificates for Graphs with Distinct Eigen Values,” by F. Thomson Leighton and Gary l. Miller, unpublished, 1979 (paper here)
Another place to learn about this, without all the smudge marks, is at the Yale course site of Dan Spielman:
- Spectral Graph Theory, Dan Spielman, Fall 2009 (course website , notes on multiplicity free graph isomorphism)
Here would be a good place to mention the general case for bounded multiplicity
- “Isomorphism of graphs with bounded eigenvalue multiplicity” by Laszlo Babai, D. Yu. Grigoryev, and David M. Mount, STOC 1982 (paper here)
Though jumping in to that paper after the previous ones is a bit of a leap.
Okay, so now your all warmed up. Indeed you’re probably so stoked that you think a polynomial time classical algorithm is just around the corner. Time to put a damper in those thoughts.
First lets start with the paper that is, currently the best algorithm for general graphs. Well actually for the original best algorithm, I’m not sure if there is an actual paper, but there is a paper which achieves a similar bound see
- “Canonical labeling of graph” by László Babai and Eugene M. Luks STOC 1983 (paper here)
This describes a subexponential (or, err, what did Scott decide to call this?),  , time algorithm for a graph with
, time algorithm for a graph with  vertices. Now as a reading list I don’t recommend jumping into this paper quite yet, but I just wanted to douse your optimism for a classical algorithm by showing you (a) the best we have in general is a subexponential time algorithm, (b) that record has stood for nearly three decades, and (c) that if you look at the paper you can see it’s not easy. Abandon hope all ye who enter?
vertices. Now as a reading list I don’t recommend jumping into this paper quite yet, but I just wanted to douse your optimism for a classical algorithm by showing you (a) the best we have in general is a subexponential time algorithm, (b) that record has stood for nearly three decades, and (c) that if you look at the paper you can see it’s not easy. Abandon hope all ye who enter?
Okay, so apparently you haven’t been discouraged, so you’re pressing onward. So what to read next?
Well one strategy would be to go through the list of all the graphs for which there are efficient known algorithms. This is quite a list, and it is useful to at least gain some knowledge of these papers, if at least to no re-solve one of these cases (above we noted the paper for bounded eigenvalue multiplicity):
- Planar graphs: “Linear time algorithm for isomorphism of planar graphs” by J.E. Hopcroft and J.K. Wong, STOC 1974 (paper here)
- or more generally graphs of bounded genus: “Isomorphism testing for graphs of bounded genus” by Gary Miller, STOC 1980 (paper here)
- Graphs with bounded degree: “Isomorphism of graphs of bounded valence can be tested in polynomial time” by Eugene M. Luks, Journal of Computer and System Sciences 25: 42–65, 1982 (paper here)
Along a similar vein, there is a subexponential time algorithm for strongly regular graphs that is better than the best general algorithm described above:
- “Faster Isomorphism Testing of Strongly Regular Graphs” by Daniel A. Spielman STOC 1996 (paper here)
At this point, you’re probably overloaded, so a good thing to do when you’re overloaded is to find a book. One interesting book is
- “Group-Theoretic Algorithms and Graph Isomorphism ” by C.M. Hoffman 1982 (link here)
As you can see this paper was written before the best algorithms were announced. Yet this book is fairly readable and begins to set up the group theory you’ll need if you want to conquer the later papers. Another book with some nice results is
- “The graph isomorphism problem: its structural complexity” by Johannes Köbler, Uwe Schöning, Jacobo Torán (1993) (buy it here)
where you will find some nice basic complexity theory results about graph isomorphism.
Well now that you’ve gone and starting learning about some computational complexity in relationship to graph isomorphism, it’s probably a good time to stop and look at actual practical algorithms for graph isomorphism. The king of the hill here, as far as I know, is the program nauty (No AUTomorphism, Yes?) by Brendan D. McKay. Sadly a certain search engine seems to be a bit too weighted to the word “naughty” (note to self, consider porn related keyword when naming a software package):
 Nauty’s main task is determining the automorphism group of a graph (the group of permutations that leave the graph representation unchanged) but nauty also produces a canonical label that can be used for testing isomorphism. Nauty can perform isomorphism tests of graphs of 100 vertices in about a second. There is an accompanying paper describing how nauty works:
Nauty’s main task is determining the automorphism group of a graph (the group of permutations that leave the graph representation unchanged) but nauty also produces a canonical label that can be used for testing isomorphism. Nauty can perform isomorphism tests of graphs of 100 vertices in about a second. There is an accompanying paper describing how nauty works:
- “Practical Graph Isomorphism”, by Brendan D. McKay, Congressus Numerantium, 30, 45-87, 1981. (paper here)
A canonical label for a graph is a function from graphs to a set of labels such that for two graphs the label is the same if and only if the two graphs are isomorphic. This is what nauty produces: if you want to know whether the graphs are isomorphic you just compute the canonical forms for these graphs and compare the results. If they have the same canonical form they are isomorphic, if they don’t they are not isomorphic.
Which leads one to thinking about other labeling schemes for solving graph isomorphism. One of the simplest attempts (attempt because it does not work) to make a canonical labeling scheme is the following: begin by labeling the vertices of the two graphs by their degrees. If you then sort this list and they are different sorted lists, then the graphs cannot be isomorphic. Next one can replace the vertex label by a label made up of the multiset of the current vertex label and the labels of the neighboring vertices (recall a multiset is a set where entries can appear multiple times.) One can then sort these multisets lexographically and compare the two sorted lists for both graphs. Again if the lists are not the same the graphs are not isomorphic. If you still haven’t discovered that the graphs are not isomorphic you can continue, but first, to keep the labels small, you should replace the lexographically ordered labels by a small integer representing the sorted order of the label. Then one can iterate the construction of a new multiset labeling from these new integer labelings. This is a simple scheme to implement. Below, for example, I perform it for two very simple graphs. First:


Next:


At which point we stop because if we compare the sorted lists of these multisets they are different (one has 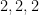 while the one on the right does not.) One can show that the above labeling procedure will always stabilize after a polynomial number of iterations (can you see why?) but also it’s quite clear that it doesn’t work in general (i.e. it doesn’t provide a canonical labeling for all graphs) since it gets stuck right off the bat with regular graphs (graphs whose degree is the same across the entire graph.) Here are two 3-regular graphs that are not isomorphic:
while the one on the right does not.) One can show that the above labeling procedure will always stabilize after a polynomial number of iterations (can you see why?) but also it’s quite clear that it doesn’t work in general (i.e. it doesn’t provide a canonical labeling for all graphs) since it gets stuck right off the bat with regular graphs (graphs whose degree is the same across the entire graph.) Here are two 3-regular graphs that are not isomorphic:


The above algorithm doesn’t even get off the ground with these non-isomorphic graphs 🙂 One can imagine, however, more sophisticated versions of the above algorithm, for example by labeling edges instead of vertices. It turns out there is a very general set of algorithms of this form, known as the k-dimension Weisfeiler-Lehman algorithm, that work along the lines of what we have described above. Boris Weisfeiler, as I mentioned in a previous post, went missing in Chile in 1985 under presumably nefarious circumstances. For a good introduction to the WL algorithm, I recommend the paper
- “On Construction and Identification of Graphs (with contributions by A. Lehman, G. M. Adelson-Velsky, V. Arlazarov, I. Faragev, A. Uskov, I. Zuev, M. Rosenfeld and B. Weisfeiler. Edited by B. Weisfeiler)”, Lecture Notes in Mathematics, 558 1976 (paper here)
The dimension 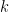 in the WL algorithm refers to whether the basic object being considered are subsets with cardinality
in the WL algorithm refers to whether the basic object being considered are subsets with cardinality 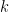 of
of  . If the k dimensional WL algorithm solved graph isomorphism for k constant, then this would give an efficient algorithm for graph isomorphism. For many years whether this was true or not was not known, and a large body of work was developed (mostly in Russia) around this method, including the introduction of topics such as cellular algebras and coherent configurations. However in 1991, Cai, Furer, and Immerman showed that this approach to efficiently solving graph isomorphism does not yield an efficient graph isomorphism algorithm. The paper where they do that is very readable and gives a good history of the WL algorithm
. If the k dimensional WL algorithm solved graph isomorphism for k constant, then this would give an efficient algorithm for graph isomorphism. For many years whether this was true or not was not known, and a large body of work was developed (mostly in Russia) around this method, including the introduction of topics such as cellular algebras and coherent configurations. However in 1991, Cai, Furer, and Immerman showed that this approach to efficiently solving graph isomorphism does not yield an efficient graph isomorphism algorithm. The paper where they do that is very readable and gives a good history of the WL algorithm
- “An optimal lower bound on the number of variables for graph identification” by Jin-Yi Cai, Martin Fürer, and Neil Immerman, Combinatorica, 12, 389-410 1991 (paper here)
At this point you might be thinking to yourself, “Hey, isn’t this the Quantum Pontiff? Where is the discussion of quantum approaches to graph isomorphism?” Okay, maybe that’s not what you’re thinking, but what the hell, now is as good as time as any to talk about quantum approaches to the problem. There are two main approaches to attacking the graph isomorphism problem on quantum computers. The first is related to the hidden subgroup problem and the second is related to state preparation and the swap test. A third “spin-off”, inspired by quantum physics also exists, which I will also briefly mention.
Recall that the hidden subgroup problem is as follows:
Hidden Subgroup Problem (HSP): You are given query access to a function 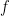 from a group
from a group  to a set
to a set  such that
such that 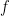 is constant and distinct on an left cosets of an unkown subgroup
is constant and distinct on an left cosets of an unkown subgroup  . Find
. Find  by querying
by querying 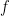 .
.
Quantum computers can efficiently (efficiently here means in a time polynomial in the logarithm of the size of the group) solve the hidden subgroup problem when the group  is a finite Abelian group. Indeed Shor’s algorithm for factoring and discrete logarithm can be seen as solving such Abelian HSPs. A nice introduction to the Abelian version of this problem, though it is now a little out of date is
is a finite Abelian group. Indeed Shor’s algorithm for factoring and discrete logarithm can be seen as solving such Abelian HSPs. A nice introduction to the Abelian version of this problem, though it is now a little out of date is
A more up to date introduction to the problem is provided by
- “Quantum algorithms for algebraic problems” by Andrew Childs and Wim van Dam, Reviews of Modern Physics 82, 1-52 2010 arXiv:0812.0380
What is the connection to the graph isomorphism problem? Well the basic result is that if one could efficiently solve the HSP over the symmetric group (or the wreath product group  ) then one would be able to efficiently solve graph isomorphism. A place to find this is in
) then one would be able to efficiently solve graph isomorphism. A place to find this is in
- “A Quantum Observable for the Graph Isomorphism Problem,” by Mark Ettinger and Peter Hoyer (1999) arXiv:quant-ph/9901029
This paper establishes that there is a measurement one can perform on a polynomial number of qubits that solves the graph isomorphism problem. Unfortunately it is not known how to efficiently implement this measurement (by a circuit of polynomial depth.) Even more unfortunately there is a negative result that says that you really have to do something non-trivial across the entire system when you implement this measurement. This is the culminating work reported in
- “Limitations of quantum coset states for graph isomorphism” by Sean Hallgren, Cristopher Moore, Martin Rotteler, Alexander Russell, and Pranab Sen, STOC 2006 (paper here)
At this point it seems that new ideas are needed to make progress along this line of attack. I have tried my own pseudo-new ideas, but alas they have come up wanting.
At this point it is useful to mention that there is a variation on the hidden subgroup problem, the hidden shift problem, which is arguably more naturally connected to the graph isomorphism problem. You can learn about this here
- “On the quantum hardness of solving isomorphism problems as nonabelian hidden shift problems,” by Andrew Childs and Pawel Wocjan, Quantum Information and Computation, 7 (5-6) 504-521, 2007 arXiv:quant-ph/0510185
I could go on and on about the hidden subgroup problem, but I think I’ll spare you.
Beyond the hidden subgroup problem, what other approaches are there to finding efficient quantum algorithms for the graph isomorphism problem? A lesser studied, but very interesting approach relates graph isomorphism to state preparation. Let 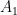 and
and  denote the adjacency matrices of the two graphs to be tested. Now imagine that we can create the states
denote the adjacency matrices of the two graphs to be tested. Now imagine that we can create the states

where  is the automorphism group of graph
is the automorphism group of graph 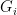 , and the sum is over all
, and the sum is over all 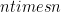 permutation matrices. Now notice that if
permutation matrices. Now notice that if 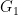 and
and  are isomorphic, then these two states are identical. If, on the other hand,
are isomorphic, then these two states are identical. If, on the other hand, 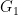 and
and  are not isomorphic then these states are orthogonal
are not isomorphic then these states are orthogonal 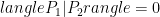 , since the superpositions above cannot contain the same term or this would yield and isomorphism. Using this fact one can use the swap test to solve graph isomorphism…given the ability prepare
, since the superpositions above cannot contain the same term or this would yield and isomorphism. Using this fact one can use the swap test to solve graph isomorphism…given the ability prepare 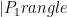 and
and 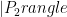 . (See here for a discussion of the swap test.) Unfortunately, no one knows how to efficiently prepare
. (See here for a discussion of the swap test.) Unfortunately, no one knows how to efficiently prepare 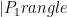 and
and 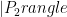 ! A good discussion, and one attack on this problem is given in the paper
! A good discussion, and one attack on this problem is given in the paper
- “Adiabatic quantum state generation and statistical zero knowledge” by Dorit Aharonov and Amnon Ta-ShmaSTOC 2003 arXiv:quant-ph/0301023
Finally let me mention a “quantum inspired” approach to graph isomorphism which has recently led to a sort of dead end, but that I find interesting. This is the approach is described in
The basic idea is as follows. As I described above, using the spectra (the list of eigenvalues) of an adjacency matrix is not enough to distinguish non-ismorphic graphs. Now the adjacency matrix is closely related to random walks on the graph being considered. Indeed from the adjacency matrix and diagonal matrix one can construct what is called the Laplacian of a graph and this is the infinitesimal generator of a random walk on the graph (I’m being sketchy here.) So thinking about this, one can ask: well what graph describes two random walkers? Well if these walkers take turns moving, then one can see that two random walkers on a graph walk on the graph described by

where 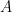 is the original one walker adjacency matrix. But of course the spectra of this new walk doesn’t help you in making a better invariant for graphs as the eigenvalues of this new walk are just the various sums of the prior eigenvalues. But, aha!, you say, what if we think like a quantum physicist and make these walkers either fermions or bosons. This corresponds to either anti-symmeterizing the above walk or symmeterizing it:
is the original one walker adjacency matrix. But of course the spectra of this new walk doesn’t help you in making a better invariant for graphs as the eigenvalues of this new walk are just the various sums of the prior eigenvalues. But, aha!, you say, what if we think like a quantum physicist and make these walkers either fermions or bosons. This corresponds to either anti-symmeterizing the above walk or symmeterizing it:

where  where
where  swaps the two subsystems. Well it is easy to check that this doesn’t help either: if you look at all of the eigenvalues of the fermion and boson walks you really just have the original eigenvalue information and no more. What Terry did, however, was to think more like a physicist. He said: well what if we consider the walkers to be bosons but now I make them what physicists call hard-core bosons (I wouldn’t recommend googling that): bosons that can’t sit on top of each other. This means that in addition to symmetrizing the
swaps the two subsystems. Well it is easy to check that this doesn’t help either: if you look at all of the eigenvalues of the fermion and boson walks you really just have the original eigenvalue information and no more. What Terry did, however, was to think more like a physicist. He said: well what if we consider the walkers to be bosons but now I make them what physicists call hard-core bosons (I wouldn’t recommend googling that): bosons that can’t sit on top of each other. This means that in addition to symmetrizing the  matrix, you also remove the part of matrix where the two walkers sit on the same vertex. Terry shows that when he does this for certain non-isomorphic strongly regular graphs that are isospectral, if he considers three walkers, the eigenvalues are no longer the same. Very cool. Some follow up papers examined this in more detail
matrix, you also remove the part of matrix where the two walkers sit on the same vertex. Terry shows that when he does this for certain non-isomorphic strongly regular graphs that are isospectral, if he considers three walkers, the eigenvalues are no longer the same. Very cool. Some follow up papers examined this in more detail
- “Symmetric Squares of Graphs” by Koenraad Audenaert, Chris Godsil, Gordon Royle, Terry Rudolph Journal of Combinatorial Theory, Series B, 97, 74-90 2007 arXiv:math/0507251
- “Physically-motivated dynamical algorithms for the graph isomorphism problem” by Shiue-yuan Shiau, Robert Joynt, and S.N. Coppersmith, Quantum Information and Computation, 5 (6) 492-506 2005 arXiv:quant-ph/0312170
(Also note another line of sort of similar investigation arXiv:quant-ph/0505026.) So does this method lead anywhere? Unfortunately the answer appears to be negative. Here is a paper
- “Spectra of symmetric powers of graphs and the Weisfeiler-Lehman refinements” by Alfredo Alzaga, Rodrigo Iglesias, and Ricardo Pignol arXiv:0801.2322
that demonstrates that the 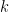 hard-core boson walker matrix provides no more information than the
hard-core boson walker matrix provides no more information than the 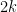 dimensional WL algorithm (which Cai, Furer, and Immerman showed cannot work. Strangely it appears that Greg Kuperberg, like Babe Ruth before him, called this one. Nice!) Recently a different approach has also emerged to showing that this doesn’t work
dimensional WL algorithm (which Cai, Furer, and Immerman showed cannot work. Strangely it appears that Greg Kuperberg, like Babe Ruth before him, called this one. Nice!) Recently a different approach has also emerged to showing that this doesn’t work
- “Non-Isomorphic Graphs with Cospectral Symmetric Powers” by Amir Rahnamai Barghi and Ilya Ponomarenko, The Electronic Journal of Combinatorics, 16(1) R120 2009 (paper here)
using the nice theory of schemes. So a good physicist inspired idea, but so far, no breakthrough.
Well I’ve gone on for a long while now. Perhaps one final reading to perform is related to graph isomorphism complete problems. Since graph isomorphism is not known to be in P nor is it known to be NP-complete, it is “natural” to define the complexity class related to graph isomorphism, GI, which is made up of problems with a polynomial time reduction to the graph isomorphism problem. Then, similar to NP-complete problems, there are GI-complete problems. Wikipedia has a nice list of such problems, but it doesn’t contain my favorite. I like this one because it doesn’t seem similar to graph isomorphism upon first reading:
- “The Complexity of Boolean Matrix Root Computation” by Martin Kutz, Theoretical Computer Science, 325(3) 373-390, 2004 (paper here)
Sadly Martin Kutz passed away in 2007 at what appears to be a quite young age, considering his condensed publication record. Read his paper for a nice square root of matrices problem that is graph isomorphism complete.
So see how much fun studying graph isomorphism can be? Okay, for some definition of fun! Please feel free to post other papers in the comment section.





















