Some motivation: which quantum many-body systems can be simulated efficiently on a classical computer? Which states even have an efficient classical description (even if we might have trouble finding that description)? Can we efficiently describe their entanglement? These questions are important both theoretically and practically.
In this talk, we’ll address this question specifically focused on the case of ground states of gapped local Hamiltonians.
We care about this special case for reasons related to both physics and computer science. Local Hamiltonians are ubiquitous in condensed matter physics, and are the natural quantum version of constraint satisfaction problems in complexity theory.
For a state to be “efficient” in a meaningful sense, we should not just have a poly-sized classical description of the state. (For example, the local Hamiltonian itself implicitly gives such a description!) We should be able to efficiently calculate the expectation values of local observables.
For an arbitrary pure state, the Schmidt rank (
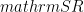
) or the von Neumann entropy (

) can be as large as the total number of spins in one half of a bipartition. In condensed matter systems we expect that these measures of entanglement don’t have a volume scaling, but rather, a scaling proportional to the number of spins on the boundary of the region defining the bipartition. This is what is meant by an area law.
Why might you expect that an area law holds? One motivation is the exponential clustering theorem (Hastings & Koma `06, Nachtergaele & Sims `06) which says that gapped systems have connected correlation functions which decay exponentially. Namely, if

is a ground state of a gapped system, then for local observables with disjoint support we have
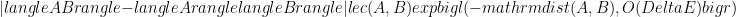
Here the constants depend on the strength of interactions and the norms of the local observables.
But correlation is not the same as entanglement! For example, there
are data hiding states (Hayden et al. `04, Hastings `07). Bouding
the entanglement length is much harder than simply bounding
correlation because, in a sense, entanglement can “sum up” a bunch of weak correlations and possibly add up to something large.
The area law has only been proven rigorously for 1d systems (Hastings `07) and it is open in other settings. For a 1D system, the area law means that the entropy of any contiguous block is bounded from above by a constant. Some implications: the ground state has an efficient description in terms of an MPS and it explains why DMRG works so well in practice.
What about dimensions higher than one? The constants in Hastings’ proof are exponential in 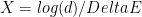 . (Here d is local site dimension.) The best lower bounds (Hastings & Gottesman `09, Irani `09) are only polynomial:
. (Here d is local site dimension.) The best lower bounds (Hastings & Gottesman `09, Irani `09) are only polynomial: 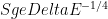 . Improving these constants in the 1d proof might be able to give nontrivial bounds in 2d by course graining one of the dimensions, so progress on these constants could have highly nontrivial implications.
. Improving these constants in the 1d proof might be able to give nontrivial bounds in 2d by course graining one of the dimensions, so progress on these constants could have highly nontrivial implications.
The new result, an upper bound which has only polynomial dependence on 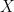 . The new bound is, up to polylog factors,
. The new bound is, up to polylog factors, 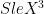 .
.
The proof techniques use Chebyshev polynomials an they might be useful elsewhere. They assume the Hamiltonian is frustration free, but this probably can be extended to the more general case of frustrated gapped local Hamiltonians.
Outline of the proof
The general strategy: start with a product state and approach the ground state without generating too much entanglement. For example, let’s assume that the projection to the ground state doesn’t create too much entanglement, as quantified by the Schmidt rank:  for some
for some  . Then we could get a bound of
. Then we could get a bound of 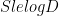 in terms of the von Neumann entropy.
in terms of the von Neumann entropy.
We will have to use an approximate ground state projector (AGSP). It needs to have three properties (here  is the unique ground state):
is the unique ground state):

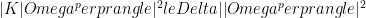

Three factors determine the bound on  :
: 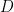 , which measures how much entanglement we create; the shrinking factor
, which measures how much entanglement we create; the shrinking factor  , which determines how fast we approach the ground state with each successive application of
, which determines how fast we approach the ground state with each successive application of 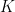 ; and
; and  , the overlap between the initial product state and the ground state.
, the overlap between the initial product state and the ground state.
Lemma: 
When 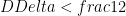 , then there is a product state with big overlap with the ground state (
, then there is a product state with big overlap with the ground state ( isn’t too small). This is the bootstrap lemma. As a corollary, then for any AGSP we have an area law.
isn’t too small). This is the bootstrap lemma. As a corollary, then for any AGSP we have an area law.
Now to prove the area law, we need to actually find a good AGSP. If it is frustration free, we can consider local projectors w.l.o.g. Then we can use the detectability lemma to get the AGSP.
The idea of the detectability lemma is to split the projectors into two layers, the product projector onto the even and odd terms in the Hamiltonian, respectively. Let  . Then we have
. Then we have
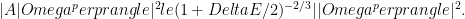
Therefore, A is an AGSP and the Schmidt rank increases by at most  and shrinkage factor satisfies
and shrinkage factor satisfies 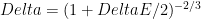 . But we need a better AGSP to get an improvement to the area law.
. But we need a better AGSP to get an improvement to the area law.
Main idea: “dilute” A a bit so that we don’t let the entanglement accumulate too much. Can we dilute A so that the Schmidt rank decreases, but without worsening the shrinking factor by too much?
We define a new operator 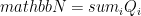 . It counts the number of constraint violations in a particular layer. It is a polynomial of degree m (the number of terms in the layer). Can we approximate it with a lower degree polynomial? Yes, and this is where the Chebyshev polynomials enter. Taking the Chebyshev polynomial of degree
. It counts the number of constraint violations in a particular layer. It is a polynomial of degree m (the number of terms in the layer). Can we approximate it with a lower degree polynomial? Yes, and this is where the Chebyshev polynomials enter. Taking the Chebyshev polynomial of degree  gives a good approximation, but with a much lower degree. But now the number of terms is large.
gives a good approximation, but with a much lower degree. But now the number of terms is large.
We have to bound the number of terms in the sum. The bound is 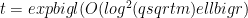 . The overall Schmidt rank is at most
. The overall Schmidt rank is at most  .
.
Now we have to glue everything together. We still have to initially course grain the system a bit to deal with the case when 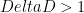 . (Recall, we need this product to be less than one half in order to get the first lemma to work).
. (Recall, we need this product to be less than one half in order to get the first lemma to work).
Open questions: efficient representation for ground states of gapped local Hamiltonians in higher dimensions? Area law for higher dimensions? Can the proof be generalized to the frustrated case? Can this idea of “dilution” be used elsewhere?
Spyridon Michalakis and Justyna Pytel:
Stability of Frustration-Free Hamiltonians
I already blogged about this work (twice!) so I’ll just refer to that.
Toby Cubitt, Martin Schwarz, Frank Verstraete, Or Sattath and Itai Arad:
Three Proofs of a Constructive Commuting Quantum Lovasz Local Lemma
The Lovász Local Lemma (LLL) says that if several events are “mostly independent”, then the probability that none of these events occurs is still strictly positive. The constructive version of the LLL, whose most recent instantiation is due to Moser and Moser & Tardos, shows that the simplest algorithm you can imagine converges to a solution: just start with a random assignment and then check random constraints which are violated, fix them with a random assignment, and repeat until you reach a satisfying assignment. The quantum version of the LLL replaces classical “events” with projectors, but the current version is nonconstructive. Can we find a constructive proof in the quantum case?
There are two challenges: entanglement and the measurement-disturbance tradeoff. This talk will focus on the challenge of entanglement, since this challenge is present even in the presence of commuting Hamiltonians.
In the simplest generalization of Moser & Tardos (probabilistic version) to the quantum case, we just replace local qubits with the maximally mixed state. This is the Verstraete et al. `09 dissipative map, so we know it converges to the correct state, but we can’t (yet) bound the convergence rate.
Key lemma: We can bound the probability of generating a particular sampling sequence, i.e. a particular directed acyclic graph (DAG). Next, we can bound the expected number of violations, then use this as a subroutine in an efficient algorithm. This allows us to bound the runtime.
Second approach: use the original entropy compression argument of Moser. This goes through without too much effort. The algorithm halts in expected linear time.
What about the noncommutative case? Now there are two complementary problems: in the first proof, we can no longer bound the runtime. In the info-theoretic second proof, there is no guarantee that it halts on the correct state (though it definitely will halt). There are two conjectures which, if true, would enable a noncommutative constructive QLLL. See the paper for details.
Toby, you went way too fast for me to keep up, sorry.
Norbert Schuch:
Complexity of commuting Hamiltonians on a square lattice of qubits
I also blogged about this one previously.
Josh Cadney, Noah Linden and Andreas Winter (contributed talk):
Infinitely many constrained inequalities for the von Neumann entropy
The speaker addresses a central question which affects all of us: Why is this talk better than lunch? Answer: it’s different; it’s introductory.
The von Neumann entropy satisfies many inequalities, for example, positivity and the strong subadditivity inequality. In this talk, we are interested only in inequalities based on reduced states that are dimension independent.
Define the entropy vector: for any subset of systems 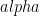 , we define reduced state on
, we define reduced state on 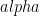 , and the associated entropy. Stack all of these entropies into one big vector. If we fix the number of parties to be n, then we let
, and the associated entropy. Stack all of these entropies into one big vector. If we fix the number of parties to be n, then we let 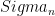 be the set of all entropy vectors of n-partite states. We don’t make restrictions on the local Hilbert space dimension. We want to characterize this entropy vector (as a function of n). Since the von Neumann entropy tells us about bipartite entanglement, than this might tell us something about multipartite entanglement.
be the set of all entropy vectors of n-partite states. We don’t make restrictions on the local Hilbert space dimension. We want to characterize this entropy vector (as a function of n). Since the von Neumann entropy tells us about bipartite entanglement, than this might tell us something about multipartite entanglement.
If we look at all 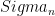 , then we get a convex cone once we take a closure. Call this the entropy cone. What sort of inequalities do we know which characterize this entropy cone?
, then we get a convex cone once we take a closure. Call this the entropy cone. What sort of inequalities do we know which characterize this entropy cone?
- For one party, we know positivity.
- For two parties, we know subadditivity and triangle inequality.
- For three parties, we know strong subadditivity and weak monotonicity.
Do these existing inequalities tell us everything we need to know about the entropy cone? To check this, we look at the extremal rays and try to find an entropy vector there. For n=2, we find that there are no more inequalities: the above list is exhaustive. For three parties, we find four families of rays, and again there are no more inequalities.
For four parties, we can continue this program. The extremal rays are stabilizer states! Are there any more four party inequalities? We don’t yet know. To help address the question, we first look at the classical case (Shannon entropy). In the classical case we additionally have (non-weak) monotonicity. Playing the same game in the classical system, we learn from previous work that the four-party cone isn’t polyhedral: there are an infinite number of entropy inequalities.
New result: given a constraint on the mutual information 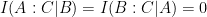 , then there are new inequalities, and additional inequalities each time we add a new party. See the paper for details. The proof elaborates on a classical proof by Makarychev et al. from `02. Each of the inequalities is independent: every new inequality sharpens the bound on the entropy cone in a different way than the others. They have not been able to violate a single one of the new classical inequalities numerically.
, then there are new inequalities, and additional inequalities each time we add a new party. See the paper for details. The proof elaborates on a classical proof by Makarychev et al. from `02. Each of the inequalities is independent: every new inequality sharpens the bound on the entropy cone in a different way than the others. They have not been able to violate a single one of the new classical inequalities numerically.
Jeongwan Haah:
Local stabilizer codes in three dimensions without string logical operators
The general problem is to find a noise-free subspace/subsystem of a physical system on which manipulations are still possible. For a many-body system, local indistinguishability (aka topological order) is stable at zero temperature, but might be fragile at nonzero temperature. Here we are focusing on the case of memory only (so, only in the ground state).
First a review of the toric code. Because the logical operators are string-like, the toric code is not stable at nonzero temperature. This talk will try to build a code which doesn’t have this drawback.
The code is defined on a cubic lattice with 2 qubits on each vertex. There are no string-like logical operators in this model. This system has an exotic ground state degeneracy which depends on the system size.
Some general considerations:
- Simple cubic lattice with m qubits per site
- t types of cubic interactions with code space dimension > 1
- No single-site logical operators
- No obvious string operator
To simplify things:
- t=2: one for X and one for Z type Paulis
- Product of all terms in the Hamiltonian should be Id
- Logical operator on a site should be Id
- Logical operator on a straight line should be Id
These conditions can be translated to linear constraint equations on the symplectic vector space of the Abelianized Pauli group. There are 64 commutation relations on a single unit cell of a cubic lattice which determine everything and there are 27 independent linear constraints (from the above considerations). There are 37 free variables, and 30 remaining equations. If you brute force solve everything, then you find there are 17 solutions.
The first code has a Z<–>X symmetry and looks like this:
Some questions: Is this model topologically ordered? What do you mean by a “string”?
To answer the first condition, use the local topological order condition from Bravyi, Hastings, Michalakis. That is, observables with local support should not be distinguishable in the ground state. One can check this condition and it is satisfied. The computation simplifies if you take advantage of the symmetries.
Let’s get a rigorous definition of “string”. This is a key contribution of this work. A string is a finite Pauli operator which creates excitations at at most two locations. Define an “anchor” to be an envelope around the excitations. The “width” is the size of the anchors, the “length” is the distance between the anchors. There are no geometric restrictions. We need to tweak this definition a bit: we need a notion of a “trivial” string segment to rule out some annoying counterexamples.
The no-strings rule: String segments of width w and length L > c w are always trivial (where c is some constant). The above code satisfies the no-strings rule with c=15.
One can prove this using the same techniques developed above to check the local TQO condition. Jeongwan calls this the eraser technique.
To understand what the no-strings rule means, you have to develop some algebraic tools. Physically, it means you can’t drag defects; you can only annihilate them and then recreate them elsewhere. Jeongwan spent some effort describing these tools, but it was way too much for me to write all of it down (well, at least if I wanted to understand any of it). You’ll have to look at his papers for details.
Jeongwan specifically showed how both the local TQO and no-strings rule could be cast in the language of algebras of polynomials to give simple proofs for the case of his codes.
Andrew Landahl, Jonas Anderson and Patrick Rice:
Fault-tolerant quantum computing with color codes
Haah’s nice code makes me want to think more about 3d
But my 3d glasses here (puts on 3d color glasses) can make 2d color codes look 3 dimensional (see top of post.)
Consider color codes. One of the codes (the square-octagon lattice code, aka the 4,8,8 lattice) has a transversal S gate.
The control model: there is a faulty gate basis consisting of X, Z, H, S, 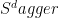 , CNOT, measurements on X and Z, and state preparations on 0, + and
, CNOT, measurements on X and Z, and state preparations on 0, + and 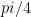 . Additional assumptions: parallel ops, refreshable ancillas, fast classical computation, equal-time gates.
. Additional assumptions: parallel ops, refreshable ancillas, fast classical computation, equal-time gates.
Locality assumptions: 2D layout, local quantum processing.
We also consider two error channels: bit flips and double Pauli (DP).
Consider three models of error:
Circuit based noise model:
- each preparation and one-qubit gate followed by BP(p)
- Each CNOT gate followed by DP(p)
- Each measurement preceded by BP(p) and result flipped with prob p
Phenomenological noise model:
- Same, except each syndrome bit extraction circuit modeled as a measurement that fails with prob p. This ignores noise propagation between data and ancilla.
One other noise model is the code capacity noise model. See paper for details. 🙂
Decoders and thresholds: Can use an MLE decoder or an optimal decoder (which might be slow). The threshold seems to be around 10.9% for the optimal decoder, and not much worse for the MLE decoder: Some numerical results (depending on model) are 10.56%, 3.05%, 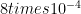 %
%

(An aside.) Random-bond Ising model: Consider an Ising model with random signs on the two-body couplings. Every CSS code has an associated random-bond Ising model. The Nishimori conjecture (which is false!) said that you can’t increase the order by increasing the temperature.
Details on syndrome extraction: One can use sequential schedules or interleaved schedules. We need to make sure that the code checks propagate to themselves, and syndrome checks propagate to themselves multiplied by a stabilizer element. They found an interleaving schedule that works.
Decoding: Use the code-capacity MLE decoder (works for all CSS codes). They formulate it as an integer program over GF(2), which can be rewritten as an integer program over the reals. (This isn’t efficient (NP-complete in general).)
Showed some pictures of the thresholds.
Turns out the interleaved schedule doesn’t have much impact… it’s about the same threshold (within error) as the sequential schedule.
Also showed some rigorous lower bounds which come from a self-avoiding walk.
Architectures and computation: can imagine a pancake architecture which does gate transversally between layers. How does this change the threshold?
Good point: Injection of magic states into codes hasn’t really been studied in the case where the injection is error-prone. This would be a good topic for future work.
Guillaume Duclos-Cianci, Héctor Bombin and David Poulin:
Equivalence of Topological Codes and Fast Decoding Algorithms
Note that I blogged about this previously.
Two gapped systems are in the same phase if there are connected by a local unitary transformation, meaning there is constant-depth quantum circuit (CDQC) which transforms one into the other.[Wen et al., 2010, Schuch et al. 2010] What makes two codes equivalent? Under what conditions does a CDQC exist?
Consider two copies of the Kitaev toric code (KTC). Does this create a new code? No… However, you could imagine applying a CDQC to the pair of codes which masks this product code. Thinking in reverse, you could ask which codes have such a character, namely, that they are loosely coupled versions of multiple copies of the KTC.
The main result is (roughly) that every 2D stabilizer code on qubits is equivalent (modulo CDQC) to several copies of the KTC, and moreover the mapping can be constructed explicitly.
Some useful concepts. Topological charges are equivalence classes of excitations which can be fused within a fixed bounded region back into the vacuum configuration. Excitation configurations are collections of defects inside a region. String operators move defects around.
The result applies in the following setting. They consider 2D lattices of qubits with geometrically local, translationally invariant stabilizer generators. To have a topological-like condition, they ask that the distance of the code scales with the linear size of the lattice ( ).
).
Gave a sketch of the proof… too detailed to blog in real time. See the paper for details.
Application to quantum error correction (QEC): The decoding problem is the same as trying to infer the worldline homology class from the measured particle configuration. You can decode, say, the 4,8,8 color code by deducing a mapping of the charges, then deducing an effective noise model on the KTCs, and then applying your favorite decoding algorithm for each KTC.
They did some numerics and found 8.7% fault-tolerance threshold for the 4,8,8 code using the RG decoder.
Joseph M. Renes, Frederic Dupuis and Renato Renner (contributed talk):
Quantum Polar Coding
Joe started off by disappointing the audience with an announcement that his all-ETHZ team had written a paper without any smooth entropies.
Instead, he talked about quantum polar codes, which are explicit, channel-adapted block quotes (CSS codes, in fact), with linear-time encoding and decoding, and achieve the symmetric (see below) coherent information for Pauli channels. They appear to need entanglement assistance, but maybe not? Details to follow.
The key idea is channel polarization. If we have two independent bits 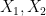 going into two bit channels with outputs
going into two bit channels with outputs 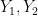 , then we can do a change of basis on the input to
, then we can do a change of basis on the input to 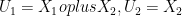 . We think of this as a channel from
. We think of this as a channel from 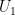 to
to  , together with a channel from
, together with a channel from 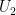 to
to  that uses our imperfect knowledge of
that uses our imperfect knowledge of 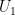 as side information. The first channel has less mutual information than our original channel, and the second channel has more. Hence we have “polarized” the channels, essentially taking the mutual information from one use and giving it to a different one.
as side information. The first channel has less mutual information than our original channel, and the second channel has more. Hence we have “polarized” the channels, essentially taking the mutual information from one use and giving it to a different one.
The basic relation is:
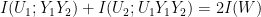
where I(W) refers to the mutual information of the original channel.
If we keep doing this recursively, we can continue until we get a bunch of nearly-perfect (good) channels and a bunch of nearly-worthless (bad) channels. Remarkably, the fraction of good channels is close to the input capacity given uniform inputs (which we call the “symmetric capacity”). To encode, we send messages over the good channels, and freeze inputs to bad channels (both parties know which ones are which). This requires only  CNOT gates. You can decode sequentially using ML; the recursive structure of the code makes ML efficient.
CNOT gates. You can decode sequentially using ML; the recursive structure of the code makes ML efficient.
The quantum version just uses the fact that the transformation is good in the conjugate basis as well! You just turn the circuit “upside-down” (CNOTs reverse the target and control). For a Pauli channel, the polarization occurs in both amplitude AND phase, albeit in different directions. We only need to analyze amplitude and phase in order to verify that a channel can send general quantum states (see Christandl & Winter 2005 for the precise statement).
Some channels are going to be good for both amplitude and phase, so we use those to send entanglement. For the ones which are bad on amplitude, we freeze the amplitude, and similarly, for the ones which are bad on phase, we freeze the phase. We can use preshared entanglement for the channels which are bad on both amplitude and phase.
To decode, just successively and coherently decode both the channels. Reuse the classical decoders. Decode first amplitude, then phase conditional on the given amplitude. You can achieve the (symmetric) coherent information as the net rate.
From the numerical simulations, (see picture) it seems that this entanglement assistance is never actually needed! 
In fact, for channels with low enough error rates they can show this rigorously. The proof techniques are similar to the original polar code proof techniques and use channel martingales.
One open question is to resolve whether or not the entanglement assistance is really necessary. Also, can they extend this to other channels? Yes! It works (joint work in progress with M. Wilde.) Plus, you can still do sequential decoding.
Sergey Bravyi and Robert Koenig:
Disorder-assisted error correction in Majorana chains
Consider, if you haven’t already, the toric code Hamiltonian 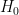 given by minus the sum of toric code stabilizer generators. Now perturb it lightly by adding local Z fields:
given by minus the sum of toric code stabilizer generators. Now perturb it lightly by adding local Z fields:  . What does the storage fidelity look like (at zero temperature) as a function of time? That is, what happens if we encode an adversarially chosen pair of qubits, wait a time t, and then try to recover the qubits? Let Tstorage denote the longest time we can wait and still get 99% fidelity.
. What does the storage fidelity look like (at zero temperature) as a function of time? That is, what happens if we encode an adversarially chosen pair of qubits, wait a time t, and then try to recover the qubits? Let Tstorage denote the longest time we can wait and still get 99% fidelity.
The bad news: 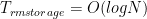 .
.
Crazy idea: Add randomness!
The idea is that the perturbation creates particles, which then hop around, creating strings that quickly lead to logical errors. But adding a little disorder can slow them down via the phenomenon of Anderson localization! In fact, the eigenfunctions can be exponentially localized. This is a nice example of a phenomenon in which something that sounds like a negative result—disorder making quantum particles move even more slowly than diffusion—turns into a postiive result, when we can use it to limit our old enemy, Eve.
Challenges: need it to work for many particles, and in 2-D. This is intractable to simulate classically.
So… instead we consider a 1D model that we can analyze, viz. unpaired Majorana modes in quantum wires (due, of course, to Kitaev).
The Hamiltonian is a sum over three types of terms: a chemical potential ( ), a hopping term (
), a hopping term (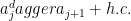 ), and a Cooper pair term (
), and a Cooper pair term (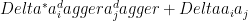 ). The base Hamiltonian has a 2-fold degenerate ground state (thus protecting a qubit). With respect to Majorana operators
). The base Hamiltonian has a 2-fold degenerate ground state (thus protecting a qubit). With respect to Majorana operators  , the Hamiltonian becomes the super simple:
, the Hamiltonian becomes the super simple:

The perturbation is 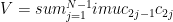 .
.
The resulting error-correction procedure resembles the minimum-weight matching procedure for the toric code, but is much simpler because it works on a line.
This code resembles the lowly repetition code, but actually has nontrivial distance.
Now what happens if the perturbation has randomly-varying weights. That is, 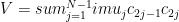 for random
for random  .
.
The expected storage time results can be summarized in the following table.
|
no disorder |
disorder |
implications |
| weak or no perturbations, with small N |
 |
 |
not so nice… |
| strong perturbations, with small N |

|
 |
nice… |
| large N |
 |
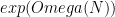 |
very nice! |
Proofs are a mix of rigorous proofs and simulation.
Dynamical localization resembles that obtained for the 1-paricle Anderson model.
 with
with 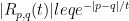 .
.
That’s only for one particle, though. They actually need to prove a bound on the expected determinant of submatrices of 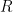 . Using this, they can show the fidelity remains high for an exponentially long time. This is interesting not only because of its implications for quantum memory, but because understanding multi-particle localization is a tough problem in general.
. Using this, they can show the fidelity remains high for an exponentially long time. This is interesting not only because of its implications for quantum memory, but because understanding multi-particle localization is a tough problem in general.
The proof uses quasi-adiabatic continuation for free fermions to argue that a superposition in the ground space is mostly preserved. Or more precisely, that the only damage occuring to it consists of correctable errors. The techniques look important and interesting. Properties such as gap stability that they prove might of interest elsewhere.
But they don’t solve everything: in some cases, they need numerical simulation. They use a number of tricks to tame the exponentials that would come from naive algorithms; in particular, taking advantage of the fact that they are working with fermionic Gaussian states (building on, and improving, an old result of Terhal and DiVincenzo).
fraction, or even a
fraction, of the total work.) A straw poll of attendees shows slight favor for Zürich. Krysta said that MSR would probably still be interested in hosting in 2018, when the geographic case for Seattle would be stronger. Neither place will be as glorious as Sydney in January, but Seattle winters are pretty mild (although gray).






